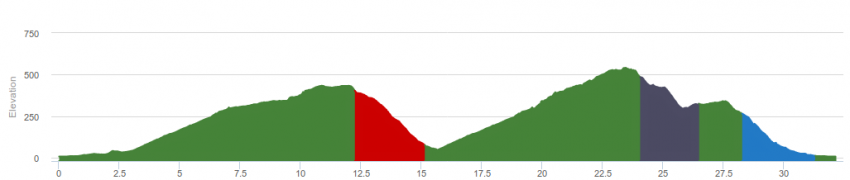
Cyclists, hikers and trail ranners know that the total elevation gain or simply elevation gain is the sum of any positive elevation change that occurs during an excursion. This is a very important parameter in the evaluation of an excursion and very difficult to evaluate correctly for the reasons that we will show you in this article.
If we have the GPS track with the elevation of the points it seems all so easy: just sums all the positive differences between all consecutive points of the track. For example, if the track consists of 10 points with the following elevations
12, 17, 15, 20, 22, 18, 15, 16, 14, 12
the elevation gain is
(17-12)+(20-15)+(22-20)+(16-15) = 14
Usually no one makes this computation by hand, what happens is that upon returning from the excursion we upload the recorded track to our favorite web service which will give us this information along with many others.
Someone will have noticed that the calculated altitude gains can differ greatly from application to application even by using the same GPS track. In the following table we show a real example obtained by listing the total positive climbs computed by four different applications from the same GPS track. For completeness, it is also shown a “rough analysis” that is obtained as described above.
| Application | Total elevation gian |
|---|---|
| GPSies | 627 |
| GPS Visualizer | 591 |
| Strava | 649 |
| Trailforks | 1208 |
| Analisi grezza | 1220 |
We notice that all the elevation gains are different and, in particular, differ from the rough analysis. This means that the four applications process the data in some way. So the question is: why it is necessary to process the data? The answer is that the data provided by the GPS devices could be inaccurate due to the typology of the gps device or the poorness of gps signals.
Device typology
Medium and high range gps devices acquire elevation data by a barometric sensor, conversely entry level devices and smart-phones determine the altitude by processing the gps signals as we shall see below. The latter method is much less accurate and so should be “fixed” in some way.
A brief description of gps technology
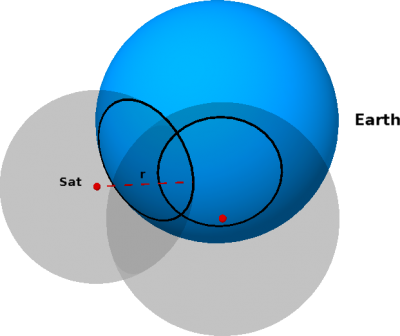
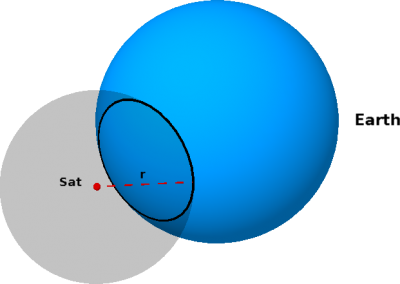
A gps device deduces its geographical position by using the position of some satellites and the time taken by the signal emitted by the satellites to reach the device. As an example we consider the case of a gps device D that receives signals from a single satellite Sat and, further simplifying, we assume that the Earth is a perfect sphere (without mountains). The signal transmitted by Sat contains a number of data, the more relevant for our example are two: (1) the one that identify Sat and its position with respect to the Earth and (2) the time t0 at which the signal has been transmitted by Sat. When D receives this signal, by using its own clock, determines the receiving time t1 and so the time t=t1-t0 spent by the signal to reach it. Since the transmission speed v of the signal is known, D can determine its distance r = vt from Sat. D can therefore deduce that it lies in the circle given by the intersection of the sphere representing the earth and the sphere of radius r and centred in the position of Sat (see the figure below).
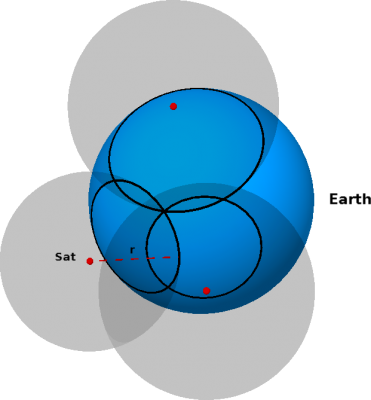
We realize that data from a single satellite are not sufficient to determine the position on the Earth, we need more satellites! If D gets informations from a second satellite, by repeating the same arguments as before, it establishes a second circle in which it can lies. Therefore, D must be in one of the two intersection points between the two circles (see the figure below on the left). In order to define the its right position, D needs data from a third satellite (see figure on the right).
Recall that we are assuming, as a simplifying hypothesis, that the Earth is a perfect sphere and so all the points in the Earth are at sea level. Therefore, in order to determine the elevation over the sea level, we need also data from a fourth satellite. Hence, to determine its position D needs at least four satellites.
In summary we can conclude that, at least from the theoretical point of view, our exact coordinates in the Earth (longitude, latitude, altitude) can be determined by receiving signals from at least four satellites simultaneously. Unfortunately, in real situations, there exist factors that can alter the received data.
- The internal clock of the device can not be perfectly accurate. In this case the computation of time t taken by the signal to reach the device is incorrect and so it is also wrong the distance r from the satellite and D.
- The presence of obstacles between satellites and devices. Obstacles like tree branches, mountains, buildings… can prevent the GPS signal to travel in a straight line; the device receives a signal that, bouncing from an obstacle to another, takes longer than necessary to reach the device. As a result, the circle computed by the device (see above) is bigger than the actual one.
In both cases the device receives or deduces an incorrect value of t. It is worth emphasizing that a microscopic discrepancy from t and its real value can cause errors of several meters. The union of all individual errors results in a GPS track that contains inaccuracies on both total length and elevation gain. However, an error of 4-500 meters on the length is less important than the same mistake made on the elevation gain! This explains why the raw elevation data from the GPS system must be corrected in some way.
Correction methods
Because of the phenomena previously described, if we draw the elevation profile of a track from its raw gps data we get a jagged curve with several sudden changes of slopes that are not encountered in reality. An efficient way to correct this issue is to smooth out the elevation curve by using statistical methods. In the next figure is represented, in red, the raw elevation profile of the Finale Ligure stage of the Enduro World Series; while, in blue, the same profile is smoothed by using a statistical filter.
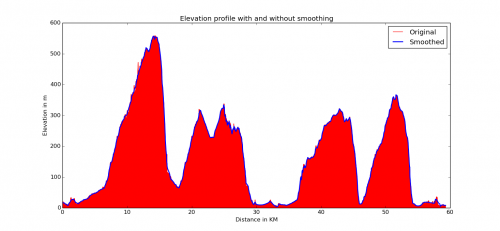
Another popular method to correct elevation data from gps uses Digital Elevation Models (DEM). A DEM is a digital representation of the Earth surface that permits to obtain the altitude above sea level from the longitude e latitude. So, the altimetric data obtained by the device are (partially or totally) ignored and substituted by those from a DEM.
The precision of the these data depends on the resolution of the DEM in question. Those freely accessible have resolutions that vary from 30 to 90 meters. In particular, in Europe, we have a resolution of 90 meters. This means that the DEM provides correct answers only in points that are vertices of a grid of squares of side length of 90 meters. The data from all the intermediate positions shall be computed through a mathematical method called interpolation.
The table shows the results obtained by applying the two methods described above against the rough analysis.
| Correction method | Total elevation gain |
|---|---|
| Smoothing filter | 1818 |
| DEM | 4331 |
| Raw analysis | 2735 |
Why the big value in the DEM line? Questions on resolution aside, the use of the DEM provides a good approximation of the actual elevation only provided that the coordinates of the point (longitude and latitude) are correct. But we know, from the above discussion, that we can not assume this: as for the elevation, we can have errors of some meters also on longitude or latitude. Even small errors on these coordinates could cause big mistakes. In order to realize this we look at an extreme example.
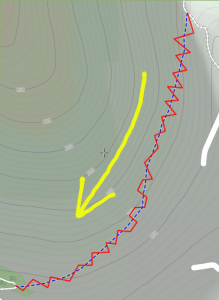
The red line represent the gps-track taken by riding the single-track (in blue) in the direction indicated by the yellow arrow. By looking at the contour lines we realize that the real elevation gain of the track should be 50 meters at most. On the contrary, if we compute the elevation gain by using the elevation data from a DEM we get a total gain of 304 meters.
This leads us to conclude that even when using the DEM we must apply a smoothing filter.
| Correction method | Total elevation gain |
|---|---|
| DEM +Smoothing | 2127 |


 Italian
Italian